Detailed Description

This class is designed to handle interpolation (resampling) of data using the ARIMA (AutoRegressive Integrated Moving Average) model.

It uses the InterpolARIMA class to perform interpolation using ARIMA, with model selection and fitting done with the ctsa (BSD-3 Clause, see below) library. That implements the auto ARIMA algorithm from Hyndman and Khandakar (2008).

Gaps in the data are detected and interpolated using the ARIMA model. If available, data before and after the gap is used to fit an ARIMA model each, one model predicting the gap forward in time, the other backward in time. A weighted average of the two predictions is then used as interpolated value. If only data is available before or after the gap, only one model is fitted and used for a prediction, either forward or backward in time.

The ARIMA model needs constant sampling rates, therefore the most likely rate is calculated in the data used to fit, and the data is resampled to that sampling rate. If a requested point falls in between available data, it will be linearly interpolated.

Missing values in the data used to fit the ARIMA Model, will be linearly interpolated as well.

A gap is defined as a period of missing data, that has at least 2 data points with the most likely sampling rate. Only 1 missing data point is linearly interpolated (should maybe just return instead).

As ARIMA is a stochastic process (white noise errors are an inherent part of the model), "prediction" needs to be specified. Here we call it a simulation, when we draw a random error for each timestep, and use the ARIMA equations (see below) to predict the proceeding values. A "prediction" is essentially the mean of many simulations, including a standard deviation (see Figure 1). As interpolated values, we only use the mean, as this is the most likely missing value, and not subject to a possible random divergence.

Note: The automatic search for the correct ARIMA model can be varyingly successfull. If it does not work, try setting the parameters manually.; You might get asked to increase the window size by a big amount, mostly when extrapolation should be done, because then the maximum of possible extrapolation steps is calculated, which might be bigger than your window size

Parameters

Mandatory parameters:

BEFORE_WINDOW : The time before a gap that will be used to accumulate data to fit the ARIMA model.
AFTER_WINDOW : The time after a gap that will be used to accumulate data to fit the ARIMA model.

Optional parameters:

MAX_P : The maximum number of AR coefficients to use in the ARIMA model. Default: 8
MAX_D : The maximum number of differences to use in the ARIMA model. Default: 3
MAX_Q : The maximum number of MA coefficients to use in the ARIMA model. Default: 8
START_P : The starting number of AR coefficients to use in the ARIMA model. Default: 2
START_Q : The starting number of MA coefficients to use in the ARIMA model. Default: 2
MAX_P_SEASONAL : The maximum number of seasonal AR coefficients to use in the ARIMA model. Default: 2
MAX_D_SEASONAL : The maximum number of seasonal differences to use in the ARIMA model. Default: 1
MAX_Q_SEASONAL : The maximum number of seasonal MA coefficients to use in the ARIMA model. Default: 2
START_P_SEASONAL : The starting number of seasonal AR coefficients to use in the ARIMA model. Default: 1
START_Q_SEASONAL : The starting number of seasonal MA coefficients to use in the ARIMA model. Default: 1
SEASONAL_PERIOD : The period of the seasonal component. Default: 0s (no seasonal component)
LIKELIHOOD_METHOD : The method used to fit the ARIMA model. Default: CSS-MLE
Options are:
- CSS-MLE : Conditional Sum of Squares - Maximum Likelihood Estimation
- ML : Maximum Likelihood Estimation
- CSS : Conditional Sum of Squares
OPTIMIZATION_METHOD : The optimization method used to fit the ARIMA model. Default: BFGS
Options are:
- BFGS : Broyden–Fletcher–Goldfarb–Shanno algorithm
- Nelder-Mead : Nelder-Mead method
- Newton_Line_Search : Newton Line Search
- Newton_Trust_Region_Hook_Step : Newton Trust Region Hook Step
- Newton_Trust_Region_Double_Dog_Leg : Newton Trust Region Double Dog Leg
- Conjugate_Gradient : Conjugate Gradient
- LBFGS : Limited Memory BFGS
- BFGS_MTM : BFGS Using More Thuente Method
STEPWISE : Whether to use stepwise search of the best ARIMA model. Default: true (faster and more robust)
APPROXIMATION : Whether to use approximation to determin the Information Criteria and the Likelihood. Default: true
NUM_MODELS : The number of models to try when using stepwise search. Default: 94
SEASONAL : Whether to use a seasonal component in the ARIMA model. Default: true
STATIONARY : Whether to use a stationary ARIMA model. Default: false
NORMALIZATION : The normalization method used to fit the ARIMA model. Default: Nothing
Options are:
- MINMAX : Min-Max Normalization
- ZSCORE : Z-Score Normalization
- NOTHING : No Normalization
VERBOSE : Whether to print additional information. Default: false

It is also possible to set the parameters of the ARIMA model manually. However, only the forward part. It is optionally supported, that a gap is filled in backwards with an auto arima model as well. Be careful when using this though, as it might lead to different results as you have been expecting. This can be done via these Keywords:

SET_MANUAL : Whether to set the ARIMA parameters manually. Default: false
FILL_BACKWARD_MANUAL : Whether to fill the gap backwards with an ARIMA model. Default: false
P : The number of AR coefficients to use in the ARIMA model. Default: 0
D : The number of differences to use in the ARIMA model. Default: 0
Q : The number of MA coefficients to use in the ARIMA model. Default: 0
P_SEASONAL : The number of seasonal AR coefficients to use in the ARIMA model. Default: 0
D_SEASONAL : The number of seasonal differences to use in the ARIMA model. Default: 0
Q_SEASONAL : The number of seasonal MA coefficients to use in the ARIMA model. Default: 0

Note: When setting the parameters manually, please provide a seasonal period, as this will now not be estimated anymore, and per default assumed to be 0.; BEWARE: The algorithm will accumulate all available data in the before and after window, so if there is another gap in this window, which might also be outside of the specified resampling area, it will just linearly interpolate the data.; The accumulation window of the data, i.e. the BEFORE_WINDOW and AFTER_WINDOW, should be chosen carefully. It has a big impact on the performance, as this will be what the ARIMA model will see.

[Interpolations1D]
TA::resample = ARIMA
TA::ARIMA::BEFORE_WINDOW = 86400
TA::ARIMA::AFTER_WINDOW = 86400

Note: In the case that only random/random walk arima models are found, the missing values will not be filled (It would be just the mean otherwise)

Introduction to ARIMA

Autoregressive Integrated Moving Average (ARIMA) is a method for forecasting on historic data. It assumes a stochastic process, with errors that are uncorrelated and have a mean of zero. The ARIMA model is a generalization of an autoregressive moving average (ARMA) which assumes stationary (statistically stable over time) data. Autoregressive refers to a prediciton based on past values of the data. Integrated refers to the differencing of the data to make it stationary. Moving average refers to the use of past errors.

To account for seasonality of the data this model can be extended to Seasonal ARIMA (SARIMA). See the following article for more information.

Model Formulation

Autoregressive (AR) Component:

The autoregressive component of order p (denoted as AR(p)) represents the correlation between the current observation and its \(p\) past observations. The general formula for AR( \(p\)) is:

\[ Y_t = \phi_1 Y_{t-1} + \phi_2 Y_{t-2} + \ldots + \phi_p Y_{t-p} + a_t \]

Here:

\(Y_t\) is the value at time t,
\(\phi_t\) are the autoregressive coefficients,
\(Y_{t-i}\) are the past observations,
\(a_t is\) a white noise term (random error) at time

Integrated (I) Component:

The integrated component of order \(d\) (denoted as I( \(d\))) is responsible for differencing the time series data to achieve stationarity. The differenced series is denoted as \(\mathbf{Y'}\) and is defined as:

\[ Y'_t = Y_t - Y_{t-d} \]

Repeat differencing d times until stationarity is achieved.

Moving Average (MA) Component:

The moving average component of order \(q\) (denoted as MA( \(q\))) represents the correlation between the current observation and \(q\) past white noise terms. The general formula for MA( \(q\)) is:

\[ Y_t = a_t - \theta_1 a_{t-1} - \theta_2 a_{t-2} - \ldots - \theta_q a_{t-q} \]

Here:

\(\theta\) are the moving average coefficients,
\(a_{t-q}\) are the past white noise terms.

ARIMA(p, d, q) Model:

Combining the AR, I, and MA components, an ARIMA( \(p, d, q\)) model is expressed as:

\[ Y'_t = \phi_1 Y'_{t-1} + \phi_2 Y'_{t-2} + \ldots + \phi_p Y'_{t-p} + a_t - \theta_1 a_{t-1} - \theta_2 a_{t-2} - \ldots - \theta_q a_{t-q} \]

Parameter Estimation

The parameters of the model are estimated by either maximising the likelihood function or minimising the sum of squared errors. The likelihood function measures the probability of observing the given data given the model parameters. Optimization is done using optimization routines like BFGS or the Nelder-Mead method.

Maximum Likelihood estimation usually gives better results but is computationally more expensive. As default a mix between the two: CSS-MLE is used, with BFGS to optimize:

TA::ARIMA::LIK_METHOD = CSS-MLE

TA::ARIMA::OPT_METHOD = BFGS

mio::ARIMAutils::BFGS

@ BFGS

Definition: ARIMAutils.h:47

mio::ARIMAutils::MLE

@ MLE

Definition: ARIMAutils.h:36

mio::ARIMAutils::CSS

@ CSS

Definition: ARIMAutils.h:37

Model Selection

Usually, the parameter selection (p, d, q)(P,D,Q) is done by minimizing the Akaike Information Criterion AIC or the Bayesian Information Criterion BIC. Which parameterize the goodness of a fit. Either an extensive search is done, i.e. all possible combinations between p=0...max_P, q=0...max_Q, ... are tried. Or a stepwise search is done, following the Implementation of Hyndman and Khandakar (2008).

As default a stepwise search is done. Additionally, an approximation of the ICs can be used to speed up the search, and the maxima of the parameters can be chosen as well.

TA::ARIMA::STEPWISE = TRUE
TA::ARIMA::APPROXIMATION = TRUE
TA::ARIMA::MAX_P = 8
TA::ARIMA::MAX_D = 3
.
.
.

In the case of a known seasonal period, e.g. yearly cycles, the seasonal component can be added to the model, by setting the seasonal period (in seconds), if it is 0 it will be estimated automatically (not always reliable):

TA::ARIMA::SEASONAL_PERIOD = 31536000

Not yet implemented: If you are familiar with finding the best ARIMA parameters via the PACF and ACF plots, you can also set the parameters manually:

TA::ARIMA::P = 2
TA::ARIMA::D = 1
TA::ARIMA::Q = 2
TA::ARIMA::P_SEASONAL = 1
TA::ARIMA::D_SEASONAL = 1
TA::ARIMA::Q_SEASONAL = 1

Forecasting and Interpolation

Forecasting is then done by using the fitted model on the available data, and predicting the next time steps. As random errors are needed, a prediction will return the mean of predicted values, and not a single simulation (one draw of the random error).

If data is available before and after a gap, two ARIMA models are fitted, one to predict forward the other to predict backward in time. A weighted average will then be computed and then used as actual prediction.

As the ARIMA model only works with constant sampling rates, the data is resampled to the most likely sampling rate. If a requested point falls in between available data, it will be linearly interpolated.

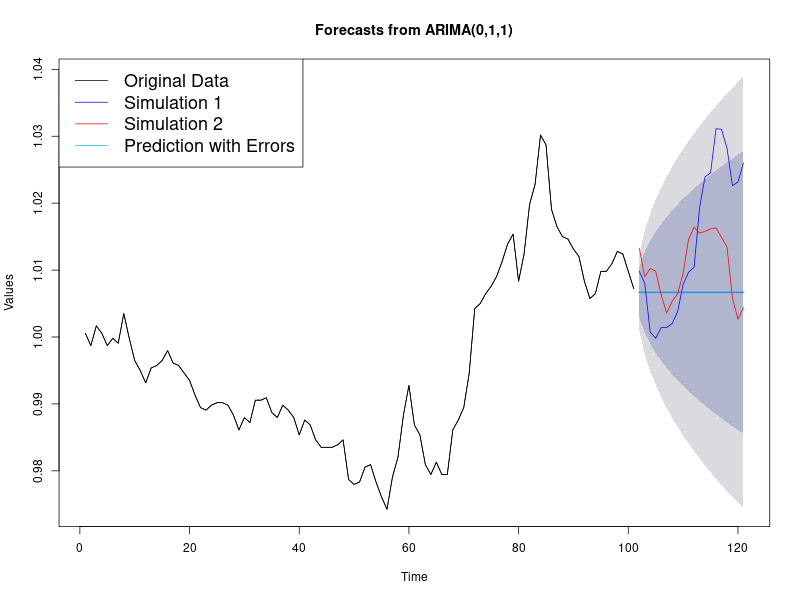
Figure 1: Prediction and Simulation using an ARIMA model.

The cyan line is the prediction (mean) with standard deviation (blue 1 \(\sigma\) and red 2 \(\sigma\)). The Blue and Red lines show two simulations, each with a different draw of random errors.

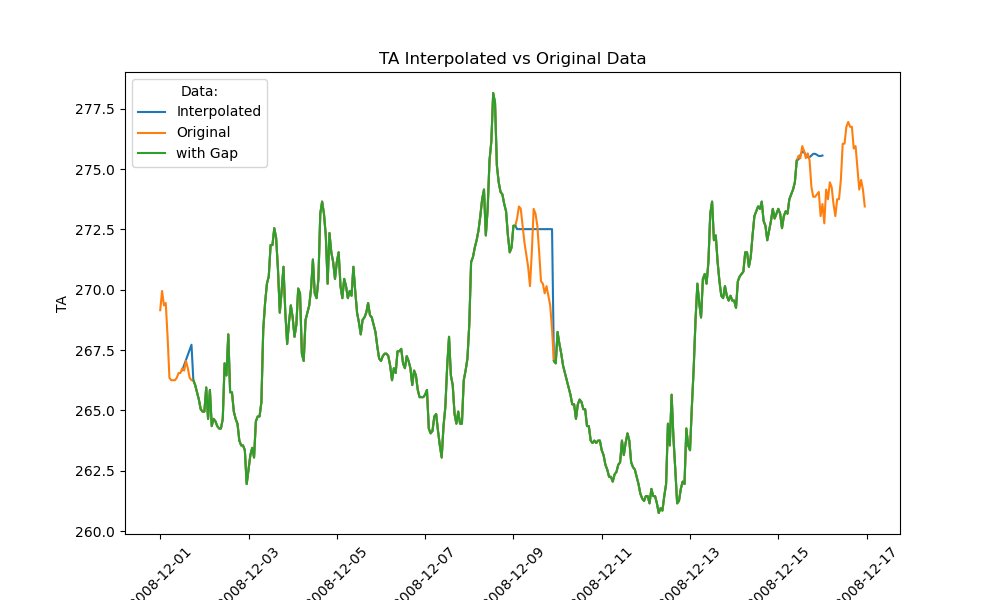
Figure 2: Interpolation using an ARIMA model.

Green shows the data given to the Interpolation Algorithm, in blue its output. And orange the original test data.

Note: The performance of the ARIMA model can vary and also depends on the given data. In general the more data the better, and when computing time is not an issue an extensive search might be useful

Author: Patrick Leibersperger

Date: 2024-01-25

Redistribution and use in source and binary forms, with or without modification, are permitted provided that the following conditions are met:

Redistributions of source code must retain the above copyright notice, this list of conditions and the following disclaimer.
Redistributions in binary form must reproduce the above copyright notice, this list of conditions and the following disclaimer in the documentation and/or other materials provided with the distribution.
The name of the author may not be used to endorse or promote products derived from this software without specific prior written permission.

THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS "AS IS" AND ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE ARE DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT HOLDER OR CONTRIBUTORS BE LIABLE FOR ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL DAMAGES (INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES; LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER CAUSED AND ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY, OR TORT (INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE OF THIS SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE.

#include <ARIMAResampling.h>

Public Member Functions
	ARIMAResampling (const std::string &i_algoname, const std::string &i_parname, const double &dflt_max_gap_size, const std::vector< std::pair< std::string, std::string > > &vecArgs)

void	resample (const std::string &stationHash, const size_t &index, const ResamplingPosition &position, const size_t &paramindex, const std::vector< MeteoData > &vecM, MeteoData &md)

std::string	toString () const

Public Member Functions inherited from mio::ResamplingAlgorithms
	ResamplingAlgorithms (const std::string &i_algoname, const std::string &i_parname, const double &dflt_max_gap_size, const std::vector< std::pair< std::string, std::string > > &)

virtual	~ResamplingAlgorithms ()

const std::string	getAlgo () const

virtual void	resample (const std::string &stationHash, const size_t &index, const ResamplingPosition &position, const size_t &paramindex, const std::vector< MeteoData > &vecM, MeteoData &md)=0

void	resetResampling ()

virtual std::string	toString () const =0

Additional Inherited Members
Public Types inherited from mio::ResamplingAlgorithms
enum	ResamplingPosition { exact_match , before , after , begin , end }

Static Public Member Functions inherited from mio::ResamplingAlgorithms
static size_t	searchBackward (gap_info &last_gap, const size_t &pos, const size_t &paramindex, const std::vector< MeteoData > &vecM, const Date &resampling_date, const double &i_max_gap_size)

static size_t	searchForward (gap_info &last_gap, const size_t &pos, const size_t &paramindex, const std::vector< MeteoData > &vecM, const Date &resampling_date, const double &i_max_gap_size, const size_t &indexP1)

static gap_info	findGap (const size_t &pos, const size_t &paramindex, const std::vector< MeteoData > &vecM, const Date &resampling_date, const double &i_max_gap_size)

Protected Member Functions inherited from mio::ResamplingAlgorithms
void	getNearestValidPts (const std::string &stationHash, const size_t &pos, const size_t &paramindex, const std::vector< MeteoData > &vecM, const Date &resampling_date, const double &i_max_gap_size, size_t &indexP1, size_t &indexP2)
	This function returns the last and next valid points around a given position. More...

Static Protected Member Functions inherited from mio::ResamplingAlgorithms
static double	partialAccumulateAtLeft (const std::vector< MeteoData > &vecM, const size_t &paramindex, const size_t &pos, const Date &curr_date)

static double	partialAccumulateAtRight (const std::vector< MeteoData > &vecM, const size_t &paramindex, const size_t &pos, const Date &curr_date)

static double	linearInterpolation (const double &x1, const double &y1, const double &x2, const double &y2, const double &x3)
	This function solves the equation y = ax + b for two given points and returns y for a given x. More...

static Date	getDailyStart (const Date &resampling_date)
	For a given date, find the start of the day, considering that for midnight we return the day before! (as is necessary for daily averages, sums, etc that can be provided at midnight for the day before) More...

static size_t	getDailyValue (const std::vector< MeteoData > &vecM, const size_t &paramindex, size_t pos, const Date &intervalStart, const Date &intervalEnd)
	Find a unique value in a given time interval. This is useful for retrieving a unique daily average, daily sum, etc. More...

Protected Attributes inherited from mio::ResamplingAlgorithms
const std::string	algo

const std::string	parname

double	max_gap_size

Static Protected Attributes inherited from mio::ResamplingAlgorithms
static const double	soil_albedo = .23
	grass albedo More...

static const double	snow_albedo = .85
	snow albedo More...

static const double	snow_thresh = .1
	These thresholds are used to handle solar radiation. More...

Constructor & Destructor Documentation

◆ ARIMAResampling()

mio::ARIMAResampling::ARIMAResampling	(	const std::string &	i_algoname,
		const std::string &	i_parname,
		const double &	dflt_max_gap_size,
		const std::vector< std::pair< std::string, std::string > > &	vecArgs
	)

Member Function Documentation

◆ resample()

void mio::ARIMAResampling::resample	(	const std::string &	stationHash,
		const size_t &	index,
		const ResamplingPosition &	position,
		const size_t &	paramindex,
		const std::vector< MeteoData > &	vecM,
		MeteoData &	md
	)

virtual

Implements mio::ResamplingAlgorithms.

◆ toString()

std::string mio::ARIMAResampling::toString ( ) const