This class implements the basic operations on matrices. Elements are access in matrix notation: that is A(1,2) represents the second element of the first line. Index go from 1 to nrows/ncols.
It might not be the best ever such implementation, but the goal is to provide a standalone matrix class. It might be later possible to chose between using the embedded implementation or to act as a front end to BLAS for those who have it installed on their system.
If the compilation flag NOSAFECHECKS is used, bounds check is turned off (leading to increased performances).
#include <Matrix.h>
Public Member Functions | |
| Matrix () | |
| Matrix (const int &rows, const int &cols) | |
| A constructor that creates a matrix of a given size. More... | |
| Matrix (const size_t &rows, const size_t &cols) | |
| Matrix (const size_t &rows, const size_t &cols, const double &init) | |
| A constructor that creates a matrix filled with constant values. More... | |
| Matrix (const size_t &n, const double &init) | |
| A constructor that creates a diagonal matrix of size n. More... | |
| Matrix (const size_t &rows, const size_t &cols, const std::vector< double > data) | |
| A constructor that takes a data vector to fill the matrix. More... | |
| void | identity (const size_t &n, const double &init=1.) |
| Convert the current matrix to a identity matrix of size n. More... | |
| void | resize (const size_t &rows, const size_t &cols) |
| void | resize (const size_t &rows, const size_t &cols, const double &init) |
| void | resize (const size_t &rows, const size_t &cols, const std::vector< double > &data) |
| void | size (size_t &rows, size_t &cols) const |
| get the dimensions of the current object More... | |
| size_t | getNx () const |
| size_t | getNy () const |
| void | clear () |
| free the memory and set the matrix dimensions to (0,0) More... | |
| void | random (const double &range) |
| fill the matrix with random numbers. More... | |
| double & | operator() (const size_t &x, const size_t &y) |
| double | operator() (const size_t &x, const size_t &y) const |
| double | scalar () const |
| Converts a 1x1 matrix to a scalar. More... | |
| Matrix | getT () const |
| matrix transpose. More... | |
| void | T () |
| Matrix | getInv () const |
| matrix invert. It first performs LU decomposition (Dolittle algorithm) and then computes the inverse by backward and forward solving of LU * A-1 = I. This inversion is in O(n³). see Press, William H.; Flannery, Brian P.; Teukolsky, Saul A.; Vetterling, William T. (1992), "LU Decomposition and Its Applications", Numerical Recipes in FORTRAN: The Art of Scientific Computing (2nd ed.), Cambridge University Press, pp. 34–42 More... | |
| bool | inv () |
| Matrix | getRow (const size_t i) const |
| Copy a matrix row to a new 1-row-matrix. More... | |
| void | setRow (const size_t i, const Matrix &row) |
| Set a matrix row from a 1-row-matrix. More... | |
| Matrix | getCol (const size_t j) const |
| Copy a matrix column to a new 1-column-matrix. More... | |
| void | setCol (const size_t j, const Matrix &col) |
| Set a matrix column from a 1-column-matrix. More... | |
| Matrix | getDiagonal () const |
| Copy the matrix diagonal to a new 1-column-matrix. More... | |
| Matrix | extract (size_t r_low, size_t r_high, size_t c_low, size_t c_high) const |
| Extract a submatrix to a new matrix. IOUtils::npos for an index means "from beginning" (i. e. 1) or "until end" (i. e. ncols resp. nrows). More... | |
| double | maxCoeff (size_t &max_row, size_t &max_col) const |
| Find the first maximum value in the matrix. More... | |
| double | det () const |
| matrix determinant More... | |
| bool | LU (Matrix &L, Matrix &U) const |
| matrix LU decomposition. Perform LU decomposition by the Dolittle algorithm, (cf http://math.fullerton.edu/mathews/numerical/linear/dol/dol.html) More... | |
| void | partialPivoting (std::vector< size_t > &pivot_idx) |
| matrix partial pivoting. This reorders the rows so that each diagonal element is the maximum in its column (see https://secure.wikimedia.org/wikipedia/en/wiki/Pivot_element) More... | |
| void | partialPivoting () |
| void | maximalPivoting () |
| void | swapCols (const size_t &j1, const size_t &j2) |
| const std::string | toString (const int &precision=2, const bool &prettify=true) const |
| Matrix & | operator+= (const Matrix &rhs) |
| const Matrix | operator+ (const Matrix &rhs) const |
| Matrix & | operator+= (const double &rhs) |
| const Matrix | operator+ (const double &rhs) const |
| Matrix & | operator-= (const Matrix &rhs) |
| const Matrix | operator- (const Matrix &rhs) const |
| Matrix & | operator-= (const double &rhs) |
| const Matrix | operator- (const double &rhs) const |
| Matrix & | operator*= (const Matrix &rhs) |
| const Matrix | operator* (const Matrix &rhs) const |
| Matrix & | operator*= (const double &rhs) |
| const Matrix | operator* (const double &rhs) const |
| Matrix & | operator/= (const double &rhs) |
| const Matrix | operator/ (const double &rhs) const |
| bool | operator== (const Matrix &) const |
| Operator that tests for equality. More... | |
| bool | operator!= (const Matrix &) const |
| Operator that tests for inequality. More... | |
| bool | isIdentity () const |
| check if a matrix is the identity matrix More... | |
Static Public Member Functions | |
| static double | scalar (const Matrix &m) |
| static double | dot (const Matrix &A, const Matrix &B) |
| Dot product. More... | |
| static Matrix | T (const Matrix &m) |
| static Matrix | solve (const Matrix &A, const Matrix &B) |
| matrix solving for A·X=B. It first performs LU decomposition and then solves A·X=B by backward and forward solving of LU * X = B More... | |
| static bool | solve (const Matrix &A, const Matrix &B, Matrix &X) |
| matrix solving for A·X=B. It first performs LU decomposition and then solves A·X=B by backward and forward solving of LU * X = B More... | |
| static Matrix | TDMA_solve (const Matrix &A, const Matrix &B) |
| Solving system of equations using Thomas Algorithm The following function solves a A·X=B with X and B being vectors and A a tridiagonal matrix, using Thomas Algorithm (see http://en.wikipedia.org/wiki/Tridiagonal_matrix_algorithm) More... | |
| static bool | TDMA_solve (const Matrix &A, const Matrix &B, Matrix &X) |
| Solving system of equations using Thomas Algorithm The following function solves a A·X=B with X and B being vectors and A a tridiagonal matrix, using Thomas Algorithm (see http://en.wikipedia.org/wiki/Tridiagonal_matrix_algorithm) More... | |
| static void | gaussElimination (Matrix &M, std::vector< size_t > &p) |
| Gaussian elimimination with partial pivoting. This function performs row reduction with (virtual) row-swapping. Attention: The original matrix is destroyed! More... | |
| static bool | gaussSolve (Matrix &M, Matrix &A, Matrix &X) |
| Equation system solver via Gaussian elimination. This function solves a set of equations M·X=A via Gauss elimination with partial pivoting. Attention: The original matrices are destroyed! More... | |
| static bool | gaussSolve (const Matrix &M, const Matrix &A, Matrix &X) |
| Convenience call to the solver with input matrix preservation. This function makes a copy of the input matrices and invokes the solver on that, i. e. they are not changed in the process. More... | |
| static bool | gaussInverse (Matrix &M) |
| Matrix inversion via Gaussian elimination. Attention: The original matrix is destroyed! More... | |
| static bool | gaussInverse (const Matrix &M, Matrix &Inv) |
| Convenience call for matrix inversion with input matrix preservation. This function makes a copy of the input matrix, i. e. it is left unchanged by the solver. More... | |
| static double | gaussDet (Matrix &M) |
| Get the matrix determinant via Gaussian elimination. Attention: The original matrix is destroyed! More... | |
| static double | normEuclid (const Matrix &vv) |
| Calculate Euclidean norm (l2) for a vector. The matrix must either be a row or a column vector. More... | |
| static unsigned int | eigenvaluesJacobi (Matrix &AA, Matrix &DD) |
| matrix bidiagonalization This uses Householder's reduction, see Golub, 1970. (see https://secure.wikimedia.org/wikipedia/en/wiki/Bidiagonalization) More... | |
| static double | jacobiEpsilon (Matrix &AA) |
| static void | svdJacobi (const Matrix &MM, Matrix &UU, Matrix &SS, Matrix &VV) |
| Singular Value Decomposition. This function calculates the SVD of a matrix. It uses an eigenvector search on M·M^T, which means problems may be squared. More... | |
| static void | sortEigenvalues (Matrix &EE, Matrix &VV) |
| static bool | isIdentity (const Matrix &A) |
Static Public Attributes | |
| static const double | epsilon = 1e-9 |
| static const double | epsilon_mtr = 1e-6 |
Protected Member Functions | |
| size_t | findMaxInCol (const size_t &col) |
| size_t | findMaxInRow (const size_t &row) |
| void | swapRows (const size_t &i1, const size_t &i2) |
Protected Attributes | |
| std::vector< double > | vecData |
| size_t | ncols |
| size_t | nrows |
|
inline |
| mio::Matrix::Matrix | ( | const int & | rows, |
| const int & | cols | ||
| ) |
A constructor that creates a matrix of a given size.
| rows | number of rows of the new matrix |
| cols | number of columns of the new matrix |
|
inline |
|
inline |
A constructor that creates a matrix filled with constant values.
| rows | number of rows of the new matrix |
| cols | number of columns of the new matrix |
| init | initial value to fill the matrix with |
| mio::Matrix::Matrix | ( | const size_t & | n, |
| const double & | init | ||
| ) |
A constructor that creates a diagonal matrix of size n.
| n | dimension of the new square matrix |
| init | initial value to fill the matrix with |
|
inline |
A constructor that takes a data vector to fill the matrix.
| rows | number of rows of the new matrix |
| cols | number of columns of the new matrix |
| data | data vector to init the matrix (must be of size rows*cols) |
| void mio::Matrix::clear | ( | ) |
free the memory and set the matrix dimensions to (0,0)
| double mio::Matrix::det | ( | ) | const |
matrix determinant
Dot product.
matrix bidiagonalization This uses Householder's reduction, see Golub, 1970. (see https://secure.wikimedia.org/wikipedia/en/wiki/Bidiagonalization)
Eigenvalue and eigenvector computation of symmetrical matrices. This function performs the iterative Jacobi method, cf. https://en.wikipedia.org/wiki/Jacobi_eigenvalue_algorithm Attention: The given matrix must be symmetrical on input!
| [in,out] | AA | The matrix to search eigenvalues for. They will be found on its diagonal after transformation (unsorted). |
| [out] | DD | Eigenvectors |
| Matrix mio::Matrix::extract | ( | size_t | r_low, |
| size_t | r_high, | ||
| size_t | c_low, | ||
| size_t | c_high | ||
| ) | const |
Extract a submatrix to a new matrix. IOUtils::npos for an index means "from beginning" (i. e. 1) or "until end" (i. e. ncols resp. nrows).
| r_low | Start from this row |
| r_high | End at this row |
| c_low | Start from this column |
| c_high | End at this column |
|
protected |
|
protected |
|
static |
Get the matrix determinant via Gaussian elimination. Attention: The original matrix is destroyed!
| [in] | M | Matrix to calculate the determinant for |
|
static |
Gaussian elimimination with partial pivoting. This function performs row reduction with (virtual) row-swapping. Attention: The original matrix is destroyed!
| [in,out] | M | The matrix to reduce |
| [out] | p | Used permutation vector (ignore p[0]) |
Convenience call for matrix inversion with input matrix preservation. This function makes a copy of the input matrix, i. e. it is left unchanged by the solver.
| [in] | M | The matrix to invert |
| [out] | Inv | The inverse matrix |
|
static |
Matrix inversion via Gaussian elimination. Attention: The original matrix is destroyed!
| [in,out] | M | The matrix to invert |
Convenience call to the solver with input matrix preservation. This function makes a copy of the input matrices and invokes the solver on that, i. e. they are not changed in the process.
| [in] | M | The matrix M in M·X=A |
| [in] | A | The solution vector (or matrix for multiple equations) A in M·X=A |
| [out] | X | The calculated solution X in M·X=A |
Equation system solver via Gaussian elimination. This function solves a set of equations M·X=A via Gauss elimination with partial pivoting. Attention: The original matrices are destroyed!
| [in] | M | The matrix M in M·X=A |
| [in] | A | The solution vector (or matrix for multiple equations) A in M·X=A |
| [out] | X | The calculated solution X in M·X=A |
| Matrix mio::Matrix::getCol | ( | const size_t | j | ) | const |
Copy a matrix column to a new 1-column-matrix.
| j | Column index |
| Matrix mio::Matrix::getDiagonal | ( | ) | const |
Copy the matrix diagonal to a new 1-column-matrix.
| Matrix mio::Matrix::getInv | ( | ) | const |
matrix invert. It first performs LU decomposition (Dolittle algorithm) and then computes the inverse by backward and forward solving of LU * A-1 = I. This inversion is in O(n³). see Press, William H.; Flannery, Brian P.; Teukolsky, Saul A.; Vetterling, William T. (1992), "LU Decomposition and Its Applications", Numerical Recipes in FORTRAN: The Art of Scientific Computing (2nd ed.), Cambridge University Press, pp. 34–42
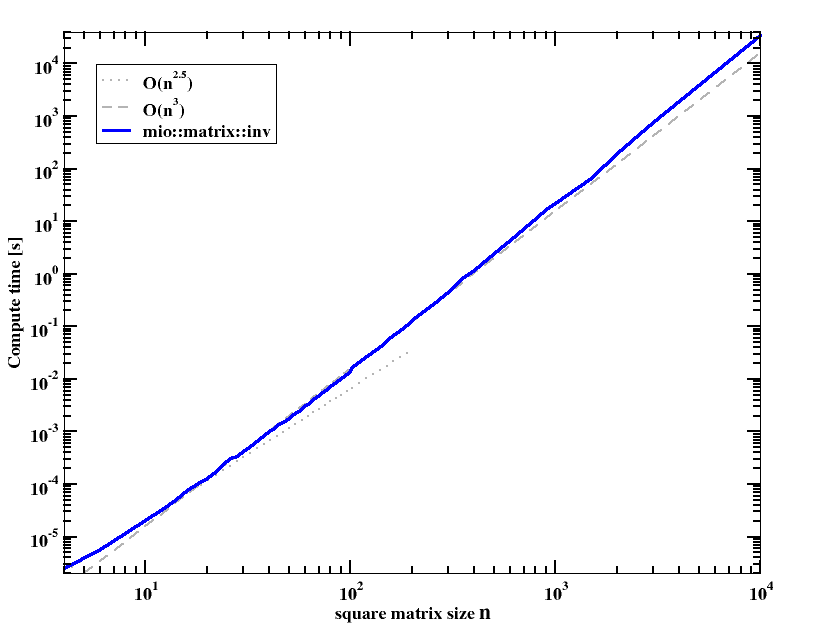
|
inline |
|
inline |
| Matrix mio::Matrix::getRow | ( | const size_t | i | ) | const |
Copy a matrix row to a new 1-row-matrix.
| i | Row index |
| Matrix mio::Matrix::getT | ( | ) | const |
matrix transpose.
| void mio::Matrix::identity | ( | const size_t & | n, |
| const double & | init = 1. |
||
| ) |
Convert the current matrix to a identity matrix of size n.
| n | dimension of the new square matrix |
| init | initial value to fill the matrix diagonal with |
| bool mio::Matrix::inv | ( | ) |
| bool mio::Matrix::isIdentity | ( | ) | const |
check if a matrix is the identity matrix
|
static |
|
static |
matrix LU decomposition. Perform LU decomposition by the Dolittle algorithm, (cf http://math.fullerton.edu/mathews/numerical/linear/dol/dol.html)
| L | lower diagonal matrix |
| U | upper diagonal matrix |
| double mio::Matrix::maxCoeff | ( | size_t & | max_row, |
| size_t & | max_col | ||
| ) | const |
Find the first maximum value in the matrix.
| max_row | Row index of the maximum |
| max_col | Column index of the maximum |
| void mio::Matrix::maximalPivoting | ( | ) |
|
static |
Calculate Euclidean norm (l2) for a vector. The matrix must either be a row or a column vector.
| [in] | vv | Vector to calculate norm for |
| bool mio::Matrix::operator!= | ( | const Matrix & | in | ) | const |
Operator that tests for inequality.
| double & mio::Matrix::operator() | ( | const size_t & | x, |
| const size_t & | y | ||
| ) |
| double mio::Matrix::operator() | ( | const size_t & | x, |
| const size_t & | y | ||
| ) | const |
| const Matrix mio::Matrix::operator* | ( | const double & | rhs | ) | const |
| Matrix & mio::Matrix::operator*= | ( | const double & | rhs | ) |
| const Matrix mio::Matrix::operator+ | ( | const double & | rhs | ) | const |
| Matrix & mio::Matrix::operator+= | ( | const double & | rhs | ) |
| const Matrix mio::Matrix::operator- | ( | const double & | rhs | ) | const |
| Matrix & mio::Matrix::operator-= | ( | const double & | rhs | ) |
| const Matrix mio::Matrix::operator/ | ( | const double & | rhs | ) | const |
| Matrix & mio::Matrix::operator/= | ( | const double & | rhs | ) |
| bool mio::Matrix::operator== | ( | const Matrix & | in | ) | const |
Operator that tests for equality.
| void mio::Matrix::partialPivoting | ( | ) |
| void mio::Matrix::partialPivoting | ( | std::vector< size_t > & | pivot_idx | ) |
matrix partial pivoting. This reorders the rows so that each diagonal element is the maximum in its column (see https://secure.wikimedia.org/wikipedia/en/wiki/Pivot_element)
| pivot_idx | new indices (to apply when solving A * X = B, for example |
| void mio::Matrix::random | ( | const double & | range | ) |
fill the matrix with random numbers.
| range | range of the randoms numbers (they will be between -range and +range) |
| void mio::Matrix::resize | ( | const size_t & | rows, |
| const size_t & | cols | ||
| ) |
| void mio::Matrix::resize | ( | const size_t & | rows, |
| const size_t & | cols, | ||
| const double & | init | ||
| ) |
| void mio::Matrix::resize | ( | const size_t & | rows, |
| const size_t & | cols, | ||
| const std::vector< double > & | data | ||
| ) |
| double mio::Matrix::scalar | ( | ) | const |
Converts a 1x1 matrix to a scalar.
|
static |
| void mio::Matrix::setCol | ( | const size_t | j, |
| const Matrix & | col | ||
| ) |
Set a matrix column from a 1-column-matrix.
| j | Column index |
| col | The new column |
| void mio::Matrix::setRow | ( | const size_t | i, |
| const Matrix & | row | ||
| ) |
Set a matrix row from a 1-row-matrix.
| i | Row index |
| row | The new row |
| void mio::Matrix::size | ( | size_t & | rows, |
| size_t & | cols | ||
| ) | const |
get the dimensions of the current object
| rows | number of rows of the matrix |
| cols | number of columns of the matrix |
matrix solving for A·X=B. It first performs LU decomposition and then solves A·X=B by backward and forward solving of LU * X = B
| A | A matrix |
| B | B matrix |
matrix solving for A·X=B. It first performs LU decomposition and then solves A·X=B by backward and forward solving of LU * X = B
| A | A matrix |
| B | B matrix |
| X | solution matrix |
Singular Value Decomposition. This function calculates the SVD of a matrix. It uses an eigenvector search on M·M^T, which means problems may be squared.
| [in] | MM | The matrix to factorize. |
| [out] | UU | Left singular vectors |
| [out] | SS | Diagonal matrix with the singular values |
| [out] | VV | Right singular vectors |
| void mio::Matrix::swapCols | ( | const size_t & | j1, |
| const size_t & | j2 | ||
| ) |
|
protected |
| void mio::Matrix::T | ( | ) |
Solving system of equations using Thomas Algorithm The following function solves a A·X=B with X and B being vectors and A a tridiagonal matrix, using Thomas Algorithm (see http://en.wikipedia.org/wiki/Tridiagonal_matrix_algorithm)
| A | A matrix |
| B | B matrix |
Solving system of equations using Thomas Algorithm The following function solves a A·X=B with X and B being vectors and A a tridiagonal matrix, using Thomas Algorithm (see http://en.wikipedia.org/wiki/Tridiagonal_matrix_algorithm)
| A | A matrix |
| B | B matrix |
| X | solution matrix |
| const std::string mio::Matrix::toString | ( | const int & | precision = 2, |
| const bool & | prettify = true |
||
| ) | const |
|
static |
|
static |
|
protected |
|
protected |
|
protected |